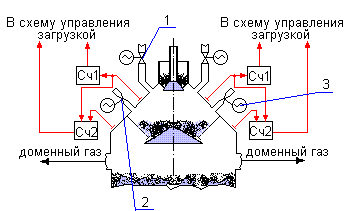
Математическое моделирование доменного процесса представляет собой сложную и многогранную задачу, требующую глубокого понимания как математических принципов, так и специфики функционирования конкретного домена. Этот процесс позволяет создавать виртуальные представления реальных систем, анализировать их поведение в различных условиях и прогнозировать их характеристики. В конечном итоге, эффективное математическое моделирование способствует оптимизации, повышению эффективности и снижению рисков в самых разных областях, от инженерии и финансов до биологии и социальных наук. В данной статье мы подробно рассмотрим ключевые аспекты математического моделирования доменных процессов, начиная с основных понятий и заканчивая практическим применением современных методов и инструментов.
Основные Понятия и Принципы Математического Моделирования
Математическое моделирование – это процесс создания математического описания реальной системы или явления. Модель представляет собой упрощенное представление реальности, которое позволяет анализировать и прогнозировать поведение системы. Основные этапы математического моделирования включают:
- Определение цели моделирования: Четкое формулирование задачи, которую необходимо решить с помощью модели. Например, оптимизация параметров производственного процесса, прогнозирование динамики популяции или анализ рисков финансового инструмента.
- Сбор и анализ данных: Получение необходимых данных о системе, включая параметры, переменные и зависимости между ними. Качество данных напрямую влияет на точность и надежность модели.
- Выбор математического аппарата: Определение подходящих математических методов и инструментов для описания системы. Это может быть использование дифференциальных уравнений, алгебраических уравнений, стохастических процессов или других математических конструкций.
- Разработка математической модели: Формулировка математических уравнений и соотношений, описывающих поведение системы. Важно учитывать упрощения и допущения, необходимые для создания адекватной и решаемой модели.
- Верификация модели: Проверка правильности реализации модели и ее соответствия заданным требованиям. Верификация включает проверку синтаксических ошибок, корректности алгоритмов и соответствия результатов моделирования ожидаемым значениям.
- Валидация модели: Оценка адекватности модели путем сравнения ее результатов с реальными данными или результатами других моделей. Валидация позволяет оценить точность и надежность модели и определить ее применимость для решения поставленной задачи.
- Анализ и интерпретация результатов: Проведение численных экспериментов с моделью, анализ полученных результатов и формулировка выводов о поведении системы. На этом этапе можно выявлять критические параметры, определять оптимальные стратегии управления и прогнозировать последствия различных сценариев.
- Применение модели: Использование модели для решения практических задач, таких как оптимизация процессов, прогнозирование, принятие решений и обучение персонала.
Типы Математических Моделей
Существует множество типов математических моделей, которые классифицируются по различным критериям:
- Детерминированные и стохастические модели: Детерминированные модели описывают системы, поведение которых полностью определяется заданными параметрами и начальными условиями. Стохастические модели учитывают случайные факторы и описывают системы, поведение которых подвержено случайным колебаниям.
- Статические и динамические модели: Статические модели описывают системы в определенный момент времени и не учитывают изменение параметров во времени. Динамические модели описывают изменение параметров системы во времени и позволяют анализировать ее поведение в динамике.
- Непрерывные и дискретные модели: Непрерывные модели описывают системы, параметры которых изменяются непрерывно во времени или пространстве. Дискретные модели описывают системы, параметры которых изменяются дискретно, например, в виде последовательности событий или состояний.
- Линейные и нелинейные модели: Линейные модели описывают системы, в которых зависимость между параметрами является линейной. Нелинейные модели описывают системы, в которых зависимость между параметрами является нелинейной.
- Аналитические и имитационные модели: Аналитические модели позволяют получить решение в виде формулы или уравнения. Имитационные модели моделируют поведение системы путем численного решения уравнений или выполнения алгоритмов.
Этапы Математического Моделирования Доменного Процесса
Математическое моделирование доменного процесса включает в себя несколько ключевых этапов, каждый из которых имеет свои особенности и требует применения определенных методов и инструментов. Рассмотрим эти этапы более подробно:
1. Постановка Задачи и Определение Целей Моделирования
На первом этапе необходимо четко сформулировать задачу, которую необходимо решить с помощью математического моделирования. Важно определить цели моделирования, например, оптимизация параметров процесса, прогнозирование его поведения, анализ рисков или разработка новых стратегий управления. Например, в доменном процессе металлургического производства целью может быть оптимизация процесса выплавки стали для снижения энергозатрат и повышения качества продукции. Четкая постановка задачи позволяет определить необходимые данные, выбрать подходящие математические методы и разработать адекватную модель.
2. Сбор и Анализ Данных
Сбор и анализ данных является критически важным этапом математического моделирования. Необходимо собрать данные о параметрах процесса, переменных и зависимостях между ними. Данные могут быть получены из различных источников, таких как экспериментальные исследования, статистические отчеты, базы данных и экспертные оценки. Анализ данных позволяет выявить закономерности, определить ключевые факторы, влияющие на поведение процесса, и оценить точность и надежность данных. Важно обеспечить качество данных, проводя очистку, нормализацию и проверку на наличие ошибок и выбросов.
3. Разработка Концептуальной Модели
Концептуальная модель представляет собой упрощенное описание системы в виде схемы или диаграммы, отражающей основные элементы системы и связи между ними. Концептуальная модель позволяет визуализировать структуру системы, определить ключевые переменные и параметры, а также сформулировать основные гипотезы о ее поведении. Разработка концептуальной модели является важным шагом к созданию математической модели, поскольку она позволяет структурировать знания о системе и определить необходимые упрощения и допущения. Например, в модели доменного процесса концептуальная модель может включать описание потоков материалов, энергии и информации, а также описание основных физических и химических процессов, происходящих в доменной печи.
4. Выбор Математического Аппарата
Выбор математического аппарата зависит от типа системы, целей моделирования и доступных данных. Для описания доменного процесса могут использоваться различные математические методы, такие как:
- Дифференциальные уравнения: Для описания динамики изменения параметров процесса во времени, например, температуры, давления и концентрации веществ.
- Алгебраические уравнения: Для описания статических зависимостей между параметрами процесса, например, уравнений материального и энергетического баланса.
- Методы оптимизации: Для определения оптимальных параметров процесса, обеспечивающих достижение заданных целей, например, минимизацию энергозатрат или максимизацию производительности.
- Статистические методы: Для анализа данных и построения эмпирических моделей, отражающих зависимости между параметрами процесса.
- Методы вычислительной гидродинамики (CFD): Для моделирования потоков газов и жидкостей в доменной печи, учитывая сложные геометрические формы и физические свойства материалов.
Выбор конкретного математического метода зависит от сложности системы, требуемой точности моделирования и доступных вычислительных ресурсов.
5. Разработка Математической Модели
На этом этапе происходит формализация концептуальной модели в виде математических уравнений и соотношений. Важно учитывать упрощения и допущения, необходимые для создания адекватной и решаемой модели. Разработка математической модели требует глубокого понимания как математических принципов, так и специфики функционирования доменного процесса. Например, модель доменного процесса может включать уравнения теплопроводности, диффузии, химической кинетики и гидродинамики. Эти уравнения могут быть решены аналитически или численно с использованием специализированного программного обеспечения.
6. Верификация и Валидация Модели
Верификация и валидация являются важными этапами математического моделирования, позволяющими оценить правильность реализации модели и ее адекватность реальной системе. Верификация включает проверку синтаксических ошибок, корректности алгоритмов и соответствия результатов моделирования ожидаемым значениям. Валидация включает сравнение результатов моделирования с реальными данными или результатами других моделей. Для валидации модели доменного процесса можно использовать данные, полученные в результате промышленных испытаний или экспериментальных исследований. Валидация позволяет оценить точность и надежность модели и определить ее применимость для решения поставленной задачи.
7. Анализ и Интерпретация Результатов
После верификации и валидации модели можно проводить численные эксперименты и анализировать полученные результаты. Анализ результатов позволяет выявить критические параметры, определить оптимальные стратегии управления и прогнозировать последствия различных сценариев. Например, с помощью модели доменного процесса можно определить оптимальные параметры загрузки шихты, расход дутья и температуру печи, обеспечивающие максимальную производительность и минимальные энергозатраты. Интерпретация результатов требует глубокого понимания как математических методов, так и специфики функционирования доменного процесса.
8. Применение Модели
Последний этап – применение модели для решения практических задач. Модель может использоваться для оптимизации параметров процесса, прогнозирования его поведения, разработки новых стратегий управления и обучения персонала. Например, модель доменного процесса может использоваться для разработки системы автоматического управления, обеспечивающей поддержание оптимальных параметров процесса в режиме реального времени. Применение модели позволяет повысить эффективность, снизить риски и улучшить качество продукции.
Примеры Математических Моделей Доменного Процесса
Существует множество различных математических моделей доменного процесса, отличающихся по сложности, точности и области применения. Рассмотрим несколько примеров:
1. Модели Термодинамического Равновесия
Эти модели основаны на законах термодинамики и описывают состояние системы в равновесии. Они используются для определения равновесного состава газов и шлаков в доменной печи, а также для оценки теплового баланса процесса. Модели термодинамического равновесия позволяют определить теоретически возможные результаты процесса, но не учитывают кинетические ограничения и динамику изменения параметров во времени.
2. Модели Кинетики Химических Реакций
Эти модели описывают скорость химических реакций, происходящих в доменной печи. Они используются для анализа влияния различных факторов, таких как температура, давление и концентрация веществ, на скорость восстановления железа из руды. Модели кинетики химических реакций позволяют учитывать кинетические ограничения и прогнозировать время достижения равновесия.
3. Модели Тепло- и Массопереноса
Эти модели описывают процессы тепло- и массопереноса в доменной печи. Они используются для анализа распределения температуры, давления и концентрации веществ в различных зонах печи. Модели тепло- и массопереноса позволяют учитывать сложные геометрические формы и физические свойства материалов, а также прогнозировать влияние различных факторов на эффективность процесса.
4. Имитационные Модели
Имитационные модели моделируют поведение доменного процесса путем численного решения уравнений или выполнения алгоритмов. Они позволяют учитывать сложные взаимодействия между различными процессами и факторами, а также анализировать поведение системы в динамике. Имитационные модели являются мощным инструментом для оптимизации параметров процесса, прогнозирования его поведения и разработки новых стратегий управления. Существуют специализированные программные пакеты для имитационного моделирования доменного процесса, такие как FactSage, HSC Chemistry и другие.
Современные Тенденции в Математическом Моделировании Доменного Процесса
Математическое моделирование доменного процесса постоянно развивается, и появляются новые методы и инструменты, позволяющие повысить точность, надежность и эффективность моделей. К современным тенденциям в математическом моделировании доменного процесса относятся:
1. Использование Методов Вычислительной Гидродинамики (CFD)
Методы CFD позволяют моделировать потоки газов и жидкостей в доменной печи с учетом сложных геометрических форм и физических свойств материалов. CFD модели позволяют анализировать распределение температуры, давления и скорости потоков в различных зонах печи, а также прогнозировать влияние различных факторов на эффективность процесса. CFD модели являются мощным инструментом для оптимизации конструкции доменной печи и разработки новых стратегий управления.
2. Применение Методов Машинного Обучения
Методы машинного обучения позволяют строить эмпирические модели на основе больших объемов данных, полученных из различных источников. Модели машинного обучения могут использоваться для прогнозирования поведения доменного процесса, оптимизации его параметров и выявления аномалий. Применение методов машинного обучения позволяет повысить точность и надежность моделей, а также автоматизировать процесс их разработки и обновления.
3. Интеграция Моделей Различных Уровней
Интеграция моделей различных уровней позволяет создать комплексную модель доменного процесса, учитывающую как микроскопические, так и макроскопические явления. Например, модель может включать описание кинетики химических реакций на микроскопическом уровне и описание тепло- и массопереноса на макроскопическом уровне. Интеграция моделей различных уровней позволяет повысить точность и надежность модели, а также получить более полное представление о поведении доменного процесса.
4. Разработка Виртуальных Двойников
Виртуальный двойник (Digital Twin) – это виртуальное представление реальной системы, которое постоянно обновляется на основе данных, полученных из реальной системы. Виртуальный двойник доменной печи может использоваться для мониторинга ее состояния, прогнозирования ее поведения, оптимизации ее параметров и разработки новых стратегий управления. Разработка виртуальных двойников является перспективным направлением в математическом моделировании, позволяющим повысить эффективность и снизить риски в доменном производстве.
Программное Обеспечение для Математического Моделирования Доменного Процесса
Существует множество программных пакетов, предназначенных для математического моделирования доменного процесса. К наиболее популярным относятся:
- FactSage: Комплексный программный пакет для термодинамического моделирования и расчета фазовых равновесий.
- HSC Chemistry: Программный пакет для термохимических расчетов и моделирования химических реакций.
- Ansys Fluent: Программный пакет для моделирования гидродинамики и теплопереноса методом конечных элементов.
- COMSOL Multiphysics: Программный пакет для моделирования различных физических процессов, включая теплоперенос, массоперенос и химические реакции.
- MATLAB: Платформа для математических вычислений, моделирования и разработки алгоритмов.
Выбор конкретного программного пакета зависит от типа моделируемого процесса, требуемой точности моделирования и доступных вычислительных ресурсов. Важно отметить, что для эффективного использования программного обеспечения требуется глубокое понимание как математических методов, так и специфики функционирования доменного процесса.
Математическое моделирование доменного процесса является мощным инструментом для оптимизации, повышения эффективности и снижения рисков в металлургическом производстве. Оно позволяет создавать виртуальные представления реальных систем, анализировать их поведение в различных условиях и прогнозировать их характеристики. Несмотря на сложность, математическое моделирование доменного процесса позволяет добиться значительных улучшений в производительности и качестве продукции. Применение современных методов и инструментов, таких как CFD, машинное обучение и виртуальные двойники, открывает новые возможности для повышения эффективности и устойчивости доменного производства. В дальнейшем, развитие математического моделирования будет направлено на создание более точных, надежных и универсальных моделей, позволяющих решать широкий круг задач в доменном производстве.
Описание: Статья посвящена подробному анализу математического моделирования доменного процесса, его этапам, типам моделей и современным тенденциям в этой области.